九州大学大学院数理学府
理学部数学科

ごあいさつ

学科紹介パンフレット

みなさん、こんにちは！
今回は理学部数学科のオープンキャンパス（のページ）を訪れていただいてありがとうございます。 ここに来られたみなさんは数学に興味があると想像します。下には、理学部数学科の先生方が数学の様々な 話題について「模擬授業」としてビデオを公開しています。 是非視聴してみて下さい。もし理学部数学科への入学に興味が湧いたら、数学科の「学科紹介パンフレット」も参考に将来への進路として是非数学科への進学を検討していただければと思います。

理学部数学科では「数学」を学び、研究します。ここで言う数学は高校で習う数学と同じで、その続きです。
しかし、一般に「大学に入って数学がわからなくなった」とか「数学科の数学は高校とは違う」という話を世間ではよく聞きますし、数学科の中でもそういう声を聞きます。 その理由は様々ですが、私思うところの一つの理由は「大学（の数学科）の数学は研究を目標としている」と言うことです。答えがあるとは限らない問題に対して、どのように問題を設定してそれを解決するかを考えるのが「研究」です。 その「研究」の際に役に立つように教えようとすると、どうしても高校とは違う教え方になります。理解を深める上では、まずは自分で時間をかけて考えた上で、先生と話したり、学生同士で議論することが必要になります。 考えたり、議論したりすることが好きな人はきっと楽しめるはずです。一方で、入試問題をパターンに沿って早く解くことが数学の上達と思っている人には少し考えを変えてもらう必要があると思います。是非、よく考えて進路を選んで下さい。

模擬授業(WEB)

ここには、九大数学科の教員による模擬授業を掲載しています。皆さんご存じの整数論や方程式に始まり、組合せ数学、折り紙、感染症数理、更に数学の様々な応用といった幅広いテーマを取り扱っています。

• 23分

  絵画の数学

  新居俊作准教授

  奥行きのある風景を平面であるキャンバスに表現するには、通常、手前のものを大きく遠くのものを小さく描きますが、具体的にどの様な比率で描いてどう並べるかを理論化したものが遠近法です。
  これは空間内の図形の配置の問題なので、そのままで理解するには(知識は小学校の算数で済むのですが)鋭い空間感覚が必要です。ここでは、高等学校で習うように「座標を用いて平面や直線を方程式で表す」という方法を用いると比較的簡単に理解できることを解説します。

• 54分

  カオス

  新居俊作准教授

  複雑で難しい問題に取り組むための一般的な指針として次があります：
  1. 問題をいくつもの小さく単純な問題の集まりに分解する。
  2. 一つ一つの単純な問題を解決する。
  3. 個々の単純な問題を組み合わせて全体をまとめる。
  科学の研究でも、このような方法論を大いに活用しています。
  この考え方には「小さく単純な問題は比較的容易に解決できる」という前提がありますが、実はこれは必ずも正しいとは限りません。
  この講義では、高校数学と高校の物理学(力学)+α の範囲で、そのような具体例を紹介します。
  (この講義で使用してるスライドは2003年度の公開講座のものなので、多少見づらい部分があります。)

• 33分

  音楽の数学I

  新居俊作准教授

  西洋音楽で使われる１２音階の歴史は古代バビロニアにまで遡りますが、近代まで基本的に比の原理に従って作られてきました。
  この講義では、古代のピタゴラス音階から現代の平均律まで、どのような原理に従って音階が作られてきたか、中学校から高等学校の初年級まで程度の数学を用いて解説します。

• 35分

  音楽の数学II

  新居俊作准教授

  「音楽の数学I」では西洋の12音階がどのように決まっているかを解説しています。
  この講義では、もう少し先に進んで、ピアノの調律がどの様な理屈に基づいて行われているかを解説します。
  「音楽の数学I」では、１オクターブ上の音は丁度２倍の周波数の音であると紹介しました。弦楽器や管楽器ではそれでいいのですが、実はピアノの調律では、１オクターブ上の音の周波数を２倍より高くしています。そうする必要が生じる理由を、弦楽器の様な柔らかい弦を振動させる場合とピアノの様な硬い弦を振動させる場合との振動の仕方の違いから解説します。
  (この講義を理解するには、高等学校３年生の理系の数学で習う三角関数の微分公式の知識が必要です。)

• 4分

  グラフ，陰関数と特異点

  大津幸男准教授

  陰関数が2変数関数から定まる場合と定まらない場合があります．そこを見極めようとしていたら…

• 7分

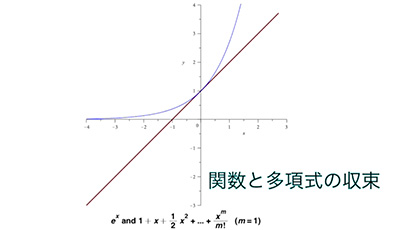
  関数と多項式の収束

  大津幸男准教授

  原点での微分を使って関数を近似する多項式を考え収束を調べると思わぬ現象が見えてきました...

• 114分

  計算可能なものと計算不可能なもの～計算理論の歴史と数理～

  浦本武雄助教

  計算理論では，「機械的に計算可能である」ことを計算モデルに基づいて厳密に定義し、「どのような命題であればその真偽を（計算モデルによる計算可能性の意味で）機械的に判定できるか」あるいは「計算可能であれば、そのために必要な計算量はどの程度か」を数学的に、定性的・定量的に議論する枠組みを与えます。
  本模擬授業では，計算理論の歴史的背景や実学的影響に触れながら，計算理論の数学的内容を概観します。

• 46分

  包除原理から　平方数とサルの動き

  石塚裕大助教

  包除原理は、集合の元を数えるときに出てくる考え方です。この模擬講義ではその整数論的な応用と、他分野における共同研究で似た考え方が現れた場面についてお話しします。

• 

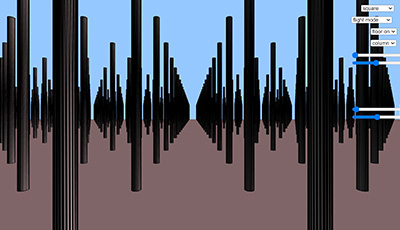
  格子の遠近法

  大津幸男准教授

  世界遺産、というより、イスラム建築の最高傑作（＊個人の感想）メスキータの多柱式礼拝堂をヒントにJavascript のライブラリー p5.jsでアプリを作成しました。
  5つある平面の二次元格子でメスキータが出来ていたとしたらどう見えるのかをご体験ください。

  上記の画像をクリックすると、別ページにて再生されます。パソコンの Chrome での使用をお奨めします。

  p5については https://p5js.org/ をご覧下さい。

• 23分

  まわれメビウス折り紙

  鍛冶静雄教授

  多くの人がきっと遊んだことのある折り紙、その背後に実は現代数学が潜んでいます。
  このビデオでは、その様子を少しだけお見せすると同時に、受験勉強ではない”学問"、そして研究者が一生をかける"仕事"としての「数学」についてもお話ししたいと思います。
  ぜひこのリンクから型紙や模型データをダウンロードして、その手で現代数学を感じてみてください。

• 24分

  3次方程式の解法1 解法

  落合啓之教授

  ２次方程式の解法の復習と y=t+1/t という魔法の変数変換で３次方程式を解きます。
  0:00２次方程式の解法の復習 7:20３次方程式でも同じように係数をどんどん綺麗にしていく 16:25係数が簡単になった３次方程式を解く 19:10もとの変数で答えを書く

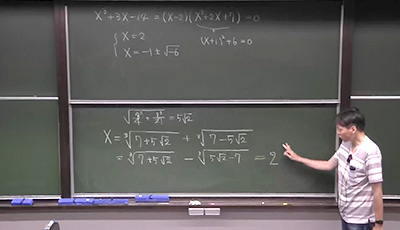• 6分

  3次方程式の解法2 解法の応用

  落合啓之教授

  この解法の応用として「驚愕の等式」と呼ばれる等式を鑑賞してみましょう。
  0:00解の公式を用いた表示：平方根や３乗根の組み合わせの複雑な表示 2:40因数分解を用いて解いた簡単な表示 5:30手品の種明かし

• 13分

  3次方程式の解法3 ガロア理論

  落合啓之教授

  解いた方程式を題材としてガロア理論の香りを嗅いでみましょう。
  0:00解いた時に用いた４つの変数の関係を整理 4:00１の３乗根によって解がどのように変化するか？ 10:30正三角形の対称性との関係

• 29分

  感染症の拡大と収束の過程の予測方法

  新居俊作准教授

  新型コロナウイルス等による感染症がどのように広がって行くかを数学的に予測する方法の基本的な考え方を高等学校の数学の範囲で解説します。

• 38分

  ネットショッピング時代の暗号理論

  新居俊作准教授

  暗号は有史以来ありますが、それらのほとんどはネットショッピング等でクレジットカード番号等の個人情報を送るには向いていません。
  そこで、インターネットでの使用に便利な暗号として「公開鍵暗号」が提唱されました。
  本講では、最初に実用化された公開鍵暗号であるRSA暗号の原理を、高等学校の数学から最小限の知識を学ぶだけで解説します。

• 5分

  アミダクジの織りなす数学

  大津幸男准教授

  アミダクジは日本発祥の籤引きですが、決まった本数のアミダクジには掛け算、単位、逆といったものが定まり、美しい数学を形作っています。
  そこから有限群論の幽玄の世界に分け入ってみましょう。

• 4分

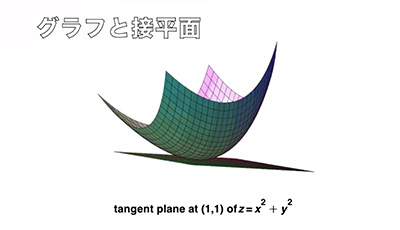
  グラフと接平面

  大津幸男准教授

  空間内の簡単な関数のグラフとその接平面たちを見くらべてみると、思いがけない関係や幾何学が見え隠れしています。

模擬授業(8月6日伊都キャンパス)概要※受講希望の方は、受付で希望の講義をお知らせください。

7月31日(月) 9:00より、一部プログラムの定員を増加いたします。
参加をご希望の方は、上記日時より追加申込を受け付けますので、予約サイトより申込をお願いいたします。
詳しくは大学のおしらせを参照ください。

九州大学オープンキャンパスサイト内の理学部のページに詳細掲載しています。
予約希望の方は、こちらから予約することができます。

リンク

• 九州大学大学院数理学府、
  理学部数学科
• オープンキャンパス特設サイト
• 九州大学